DURATION OF THE PROJECT 2023-2026

Following Gentzen's seminal paper in 1935, a logic can be characterized as a sequent calculus, that is, as a set of rules linking consequence statements (known as sequents). Thus, for example, from the statement that 'A implies B' we can infer that 'A and C implies B', expressed in sequent form:

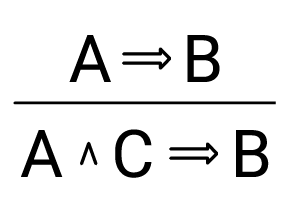
The rule allows to move from a sequent statement to a sequent involving a new piece of vocabulary (in this case, a conjunction). Other rules allow us to introduce other pieces of logical vocabulary – like disjunctions, negations and conditionals. Now, in addition to operational rules, i. e., rules introducing logical vocabulary, a sequent calculus includes structural rules, i. e., rules that don't mention any logical vocabulary. Examples of such rules are weakening and contraction,

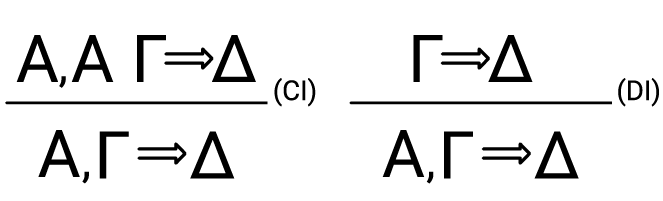
The EU-funded project PLEXUS seeks to deepen our understanding of the phenomenon of substructurality with particular emphasis on radically substructural logics: logics that can fail to be reflexive or transitive.

The first tells you that the number of occurrences of a premise is irrelevant for logical consequence, the second that adding premises to a valid argument, renders a valid argument. Operational rules can be viewed as giving the specific meaning of logical constants, while Structural rules can be viewed as encoding a structural property of the consequence relation itself.

In Gentzen's paper, Classical Logic is characterized by the sequent calculus known as LK that includes a number of structural and operational rules. LK is the paradigm of a structural logic: a logic is substructural when some structural rule of LK fails for it (or doesn't hold in full generality).

Now it is well known that Classical Logic seems inadequate to handle several phenomena – like the vagueness of natural language or semantic paradoxes. Substructural logics provide a fruitful environment for the study of alternatives to classical logic where phenomena such as vagueness or semantic paradoxes can be accommodated. Besides, the existence of substructural logics raise several philosophical questions like to what extent the absence of a structural rule affects the meaning of a logical constant.

Overall Methodology

The overall scientific methodology of the project is pluralist, as mandated by the inherently interdisciplinary character of the study of logic, which requires deploying resources from philosophy (conceptual analysis and engineering, constructive explanation, etc.), logic proper (devising and applying different proof systems, model-theoretic techniques for building counterexamples, etc.) and various branches of mathematics (e.g., algebra and set theory). Additionally, via Objective 3, the project has a significant experimental and thus empirical component, requiring specific methods and techniques of data gathering, quantitative and qualitative analysis, modelling, etc. These different methodological approaches are balanced and integrated through the construction of the WPs and the distribution of the afferent secondments (28,6% in WP1, 47,7% in WP2 and 23,5% in WP3).

knowledge As mentioned above, the guiding concepts of network PLEXUS areintegration,cross-fertilization andknowledge-sharing. As mentioned above, the driving concepts of the PLEXUS network are integration, cross-fertilisation and knowledge-sharing. We seek specifically to achieve a system of epistemic checks and balances, apt to mitigate the risk of fragmentation of the project due to bias and partisanship. For this reason, while each WP has a certain methodologically dominant characteristic, this is counterbalanced by approaches and techniques specific to subsidiary and overlapping methodological families:

W1, corresponding to Objective 1, aims to lay the groundwork for an updated philosophical analysis of substructurality, consonant with the recent formal developments. Its dominant methodology will thus be philosophical in nature and it will draw on resources from philosophical disciplines like metaphysics (conceptual analysis), philosophy of language (formalisation), philosophy of mathematics (modelling). Logico-mathematical methods (largo sensu, i.e., proof systems, theories of equivalence of logical theories, semantic frameworks) will be deployed in order to (i) inform and direct the philosophical analysis; (ii) explicitate, enrich, and ultimately verify its assumptions and results.

WP2, corresponding to Objective 2, has a predominantly formal component, being geared towards the production of logico-mathematical results such as a generalisation of model-theoretic semantics and proof-systems (natural deduction, sequent calculi, and more) for radically substructural logics, as well as the development and study of substructural theories of truth, validity, grounding, conditionals, and more related notions. Methodologically, these tasks are tantamount to developing logical tools for extending the analysis of substructurality. Subsidiarily, the development of these tools will require philosophical methods (explanation, analysis, etc.) in order to (i) guide the production of these tools; (ii) ensure that they possess desirable philosophical traits (and expose deficiencies in this regard)

The methodology of WP3 involves particular difficulties. This objective requires adapting existing methodologies in Quantitative Psychology and Computer Science to substructural logics. Quantitative Psychology will be necessary for constructing and validating the metainferences inventory. The goal of this psychometric tool will be to assess preferences on substructural logics in the general population. Our departing model is the Free Will Inventory 29-item psychometric tool designed for measuring beliefs about free will (determinism, dualism, and related constructs) with good internal consistency and construct validity evidence. In order to find an appropriate formulation of the inventory that provides sensible information about naïve speakers' inferences we will develop an iterative process of conceptualization, design, pretesting and debriefing. This process involves essential use of citizens in the final design of the tool. WP3 requires, in addition, expertise from Computer Science in order to develop an automatic theorem prover capable of handle the logics that are the main focus of this project.